Nekem mindig csak átmenőm volt matekből, de szerintem egy próbát megér.
1 millió dollárért?
3^0 + 2^2 = 5^1
azaz: 1 + 4 = 5
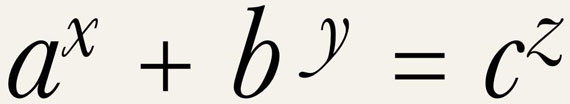
Akar egymillió dollárt keresni?
Egymillió dollárt ajánlott fel Andrew Beal texasi milliárdos bankár és műkedvelő matematikus egy húsz éve megoldatlan matematikai probléma, a saját magáról elnevezett Beal-sejtés bizonyításáért vagy cáfolatáért. A sejtést a 350 év alatt megoldott nagy Fermat-tétel inspirálta, és maga a kérdés feltevése annyira egyszerűen hangzik, hogy még matek érettségi sem kell ahhoz, hogy az ember megértse a feladatot - éppen ezért ennyire izgalmas, hogy a probléma 1993-as felvetése óta senkinek nem sikerült azt megoldania.
Terias 2013. 06. 09. 22:56 | #19
A sejtés pontosan úgy szól, ahogy leírtad:
Ha FENNÁLL az A^x + B^y = C^z egyenlőség, ahol A, B, C tetszőleges pozitív egészek, x, y, z pedig 2-nél nagyobb egész számok, AKKOR A-nak, B-nek és C-nek van közöz prímosztójuk.
Az általad említett 4^3 + 3^3 = 12^3 „valami” nem felel meg a feltételeknek, hisz 4^3+3^3 az 64+27=91, míg 12^3=1728, így itt az egyenlőség sem áll fenn. Az, hogy a kitevők nagyobbak legyenek 2-nél azért kell, hogy kikerüljük a Pitagoraszi számhármasokat, hisz például 3^2+4^2=5^2 teljesük, 3,4,5-nek mégsincs közös prímosztójuk. Épp ezért feltették, hogy x,y,z mindegyike legalább 3. Ha a kitevők ugyanazok, akkor Andrew Wiles belátta, hogy nincs a triviálistól különböző megoldás („nagy” Fermat-tétel), tehát elég azt az esetet vizsgálni, mikor x,y és z közül legalább az egyik különböző.
Egy példa amikor minden feltétel teljesül: 7^6 + 7^7 = 98^3. Itt fennáll az egyenlőség, a kitevők 2-nél nagyobbak és minden pozitív egész és látható, hogy mindegyik alapot osztja a 7. Nos, valami hasonlót kéne belátni minden létező megoldásról, vagy mutatni egy ellenpéldát, ahol TELJESÜL MINDEN feltétel, az alapoknak mégsincs közös prímosztójuk.
Ha FENNÁLL az A^x + B^y = C^z egyenlőség, ahol A, B, C tetszőleges pozitív egészek, x, y, z pedig 2-nél nagyobb egész számok, AKKOR A-nak, B-nek és C-nek van közöz prímosztójuk.
Az általad említett 4^3 + 3^3 = 12^3 „valami” nem felel meg a feltételeknek, hisz 4^3+3^3 az 64+27=91, míg 12^3=1728, így itt az egyenlőség sem áll fenn. Az, hogy a kitevők nagyobbak legyenek 2-nél azért kell, hogy kikerüljük a Pitagoraszi számhármasokat, hisz például 3^2+4^2=5^2 teljesük, 3,4,5-nek mégsincs közös prímosztójuk. Épp ezért feltették, hogy x,y,z mindegyike legalább 3. Ha a kitevők ugyanazok, akkor Andrew Wiles belátta, hogy nincs a triviálistól különböző megoldás („nagy” Fermat-tétel), tehát elég azt az esetet vizsgálni, mikor x,y és z közül legalább az egyik különböző.
Egy példa amikor minden feltétel teljesül: 7^6 + 7^7 = 98^3. Itt fennáll az egyenlőség, a kitevők 2-nél nagyobbak és minden pozitív egész és látható, hogy mindegyik alapot osztja a 7. Nos, valami hasonlót kéne belátni minden létező megoldásról, vagy mutatni egy ellenpéldát, ahol TELJESÜL MINDEN feltétel, az alapoknak mégsincs közös prímosztójuk.
0
VÁLASZ
BundasTm 2013. 06. 09. 22:42 | #18
Csak két alapvető dolgot nem vettél figyelembe.
1. Az egyenlőség jel tényleg nem viccből van ott,
2. A képlet nem A^x + B^x=C^x, hanem A^x + B^y = C^z, vagyisd a kitevő is mind más, tehát szerintem x!=y!=z (persze külön kikötve nem láttam, de gondolom nem véletlen van külön változóval jelölve, és nem ugyanazzal...)
1. Az egyenlőség jel tényleg nem viccből van ott,
2. A képlet nem A^x + B^x=C^x, hanem A^x + B^y = C^z, vagyisd a kitevő is mind más, tehát szerintem x!=y!=z (persze külön kikötve nem láttam, de gondolom nem véletlen van külön változóval jelölve, és nem ugyanazzal...)
0
VÁLASZ
Randal Graves 2013. 06. 09. 16:03 | #16
Az N=NP is sokat ér még.
Csak annyit, hogy aki megoldja, az nem fogja kérni a pénzt. :)
Csak annyit, hogy aki megoldja, az nem fogja kérni a pénzt. :)
0
VÁLASZ
adam10603 2013. 06. 08. 14:42 | #14
A^x + B^y = C^z
"Ahol A, B, C, x, y, z mind pozitív egész számok. Az amerikai matematikus sejtése az, hogy ha az egyenlet fennáll és x, y és z nagyobb mint 2, akkor a-nak, b-nek és c-nek van közös prímosztója. Ezt kellene bebizonyítani, vagy ellenpéldát találni pozitív egész számokkal."
Szerintem vagy valamit rosszul fordítottak, vagy csak én nem értem a lényeget. Itt van pl. ez:
4^3 + 3^3 = 12^3
minden szám az egyenletben pozitív egész, x,y és z nagyobbak mint 2, és az egyenlőség igaz. Tehát ez az egyenlet minden előfeltételnek megfelel. Viszont A-nak B-nek és C-nek itt nincs közös prímosztója... ha jól értelmezem a szót. Elvileg ennek egy prímszámnak kéne lenni amivel mind a hármat maradék nélkül el lehet osztani. Ilyen prímszám ebben az esetben nincs!
Mivel ez meglepően könnyű, nem hinném hogy ezért járna a lóvé, inkább én értek valamit félre. Valaki felvilágosítana hogy hol itt a baki? :D
"Ahol A, B, C, x, y, z mind pozitív egész számok. Az amerikai matematikus sejtése az, hogy ha az egyenlet fennáll és x, y és z nagyobb mint 2, akkor a-nak, b-nek és c-nek van közös prímosztója. Ezt kellene bebizonyítani, vagy ellenpéldát találni pozitív egész számokkal."
Szerintem vagy valamit rosszul fordítottak, vagy csak én nem értem a lényeget. Itt van pl. ez:
4^3 + 3^3 = 12^3
minden szám az egyenletben pozitív egész, x,y és z nagyobbak mint 2, és az egyenlőség igaz. Tehát ez az egyenlet minden előfeltételnek megfelel. Viszont A-nak B-nek és C-nek itt nincs közös prímosztója... ha jól értelmezem a szót. Elvileg ennek egy prímszámnak kéne lenni amivel mind a hármat maradék nélkül el lehet osztani. Ilyen prímszám ebben az esetben nincs!
Mivel ez meglepően könnyű, nem hinném hogy ezért járna a lóvé, inkább én értek valamit félre. Valaki felvilágosítana hogy hol itt a baki? :D
0
VÁLASZ
Felcser_HUN 2013. 06. 07. 21:14 | #12
Bannye, mit nem lehet ezen érteni? A helyes válasz: 42. Ide a zsét! :-D
0
VÁLASZ
.::JunKieEQ::. 2013. 06. 07. 14:38 | #9
Elég sok innovációt köszönhetünk a LSD-nek.... ;) De hiába.... egy szűk agynak nehéz megértenie, mit is jelent a nyitott elme...
0
VÁLASZ
.::JunKieEQ::. 2013. 06. 07. 14:04 | #7
145.... ;) Egyébként x=y=z.... Minek ezt túlbonyolítani... :DDDD
0
VÁLASZ
HeavyCross 2013. 06. 07. 13:58 | #6
Nah Junkie, ha nem meszkalinoztad volna el az agyadat, akkor most a 175-ös IQ-dat felhasználhatnád, hogy meggazdagodj :P
0
VÁLASZ
paganmantis 2013. 06. 07. 13:06 | #5
Valóban, tényleg hülyeséget hoztam fel példának. De előtte szerintem helyes amit leírtam.
0
VÁLASZ
paganmantis 2013. 06. 07. 11:22 | #1
A cikk írója mily bátran állítja, hogy érettségi sem kell a megértéséhez, csakhogy ha matekból nem is, angolból nem ártana.
Merthogy a sejtés így szól:
If Ax + By = Cz, where A, B, C, x, y and z are positive integers and x, y and z are all greater than 2, then A, B and C must have a common prime factor.
Tehát ha A,B,C,x,y,z pozitív egészek és kettőtől nagyobbak ÉS ha igaz az egyenlőség, AKKOR A,B,C-nek kell lennie közös osztójának.
Az alább leírt feltételek egyáltalán nem elégítik ki az egyenlőség feltételét is.
"Ahol A, B, C, x, y, z mind pozitív egész számok, x, y és z nagyobbak 2-nél, és A, B, és C-nek van közös osztójuk. Az amerikai matematikus sejtése az, hogy az egyenlet minden számra igaz..."
Ellenpélda: 3^3+5^3 != 21321343^4
Merthogy a sejtés így szól:
If Ax + By = Cz, where A, B, C, x, y and z are positive integers and x, y and z are all greater than 2, then A, B and C must have a common prime factor.
Tehát ha A,B,C,x,y,z pozitív egészek és kettőtől nagyobbak ÉS ha igaz az egyenlőség, AKKOR A,B,C-nek kell lennie közös osztójának.
Az alább leírt feltételek egyáltalán nem elégítik ki az egyenlőség feltételét is.
"Ahol A, B, C, x, y, z mind pozitív egész számok, x, y és z nagyobbak 2-nél, és A, B, és C-nek van közös osztójuk. Az amerikai matematikus sejtése az, hogy az egyenlet minden számra igaz..."
Ellenpélda: 3^3+5^3 != 21321343^4
0
VÁLASZ












Jó dolga van egyeseknek. Kiagyalnak szögfüggvényeket, logaritmusokat, integrálokat. Még pénzt is kapnak érte.
Nekünk, melósoknak marad a centiméter-szalag, vízszintező, függőón, kiló helyett fél lapátnyi, stb. :)